深度学习是机器学习的一种。机器学习是指对某一任务T而言的表现P能随着经验E的增长而越来越好的计算机程序¹。任务T可以多种多样，如回归（学习一个\(\mathbb{R}^n\rightarrow\mathbb{R}\)的映射）、分类、聚类、异样检测、结构化输出、降噪等。根据经验E的不同，可以从一个角度将机器学习划分为有监督学习（supervised learning，例如输入数据带有标签)和无监督学习（unsupervised learning）。但数学上讲，有监督学习和无监督学习实际上是一件事情。

机器学习中，既要使算法能够拟合到训练集，又要使算法能有泛化的能力。即，既要使 training error 尽可能小，又要使 traning error 和 test error 之间的间隔尽可能小。training error 大，即所谓的欠拟合（underfitting)，而在训练集上的 error 很小而在测试集上误差很大的现象称为过拟合（overfitting）。

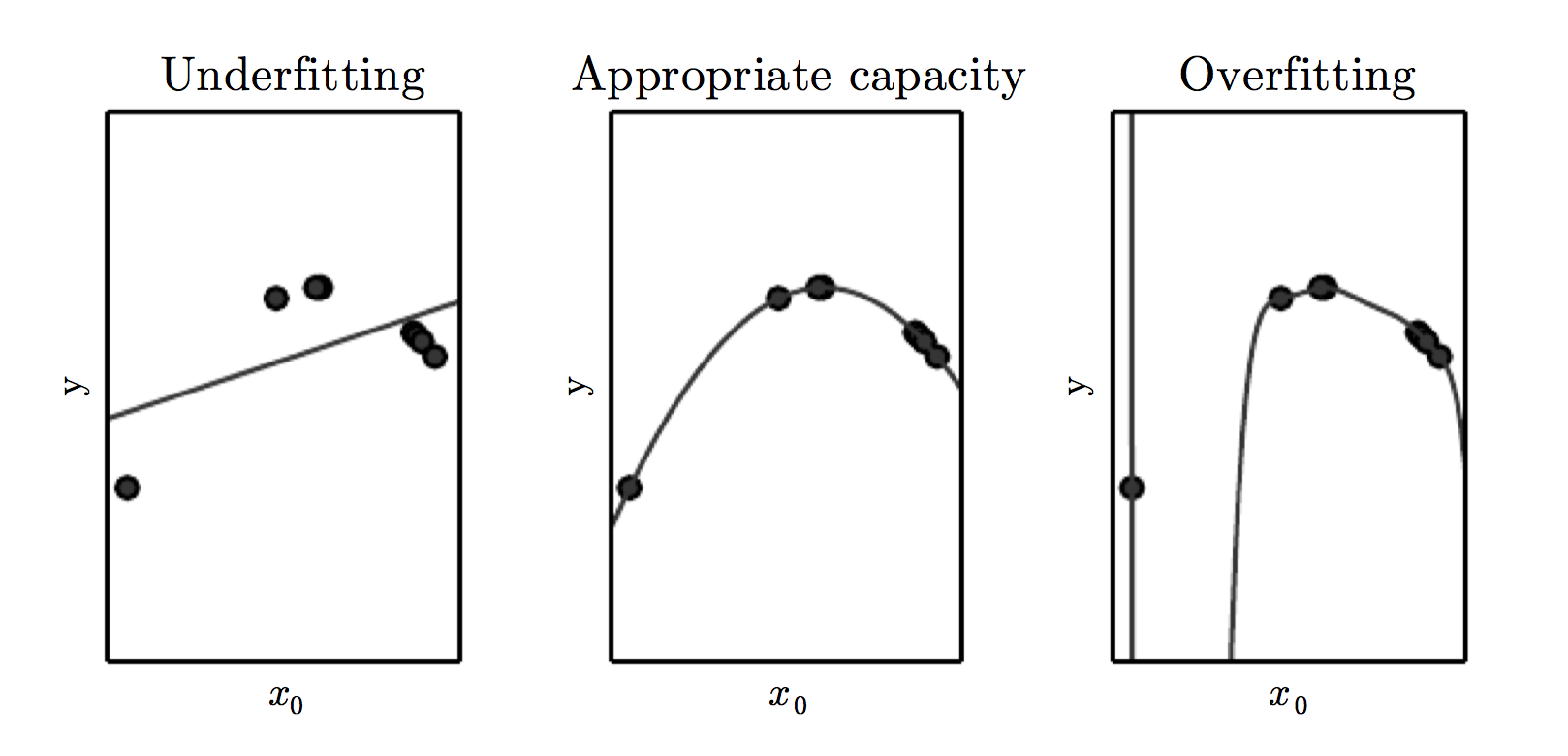
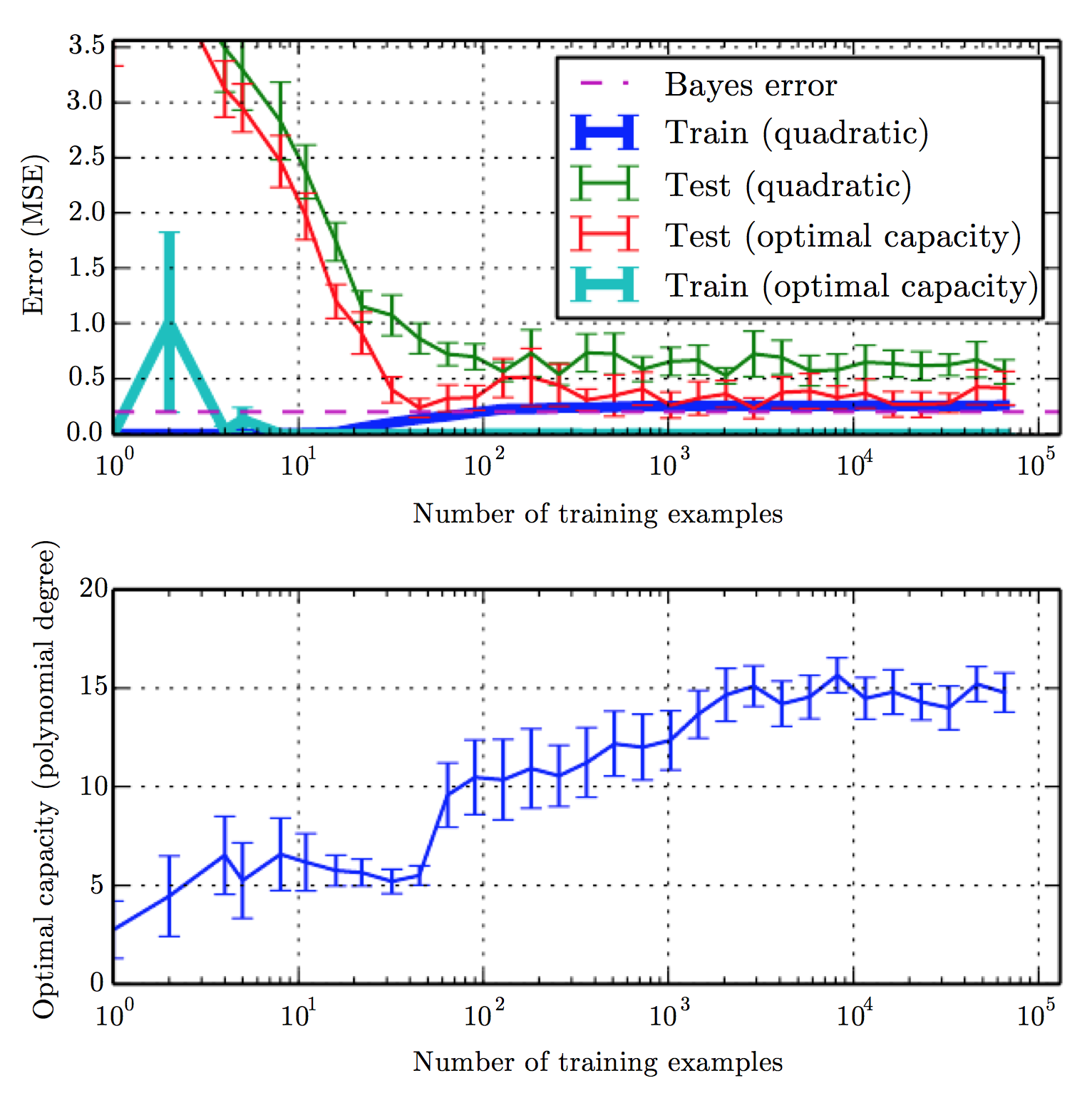
统计学习的研究表明，泛化误差（generalization error）和训练误差（traning error）之间的差距的上界随着模型表达能力（capacity）的增加而增加，随着训练数据的增多而降低。由于数据产生时不是严格按照某种概率分布（有noise）而产生的无法避免的误差称为 Bayes error。

统计学习的目标是学习一个estimator，尽可能地逼近数据产生的概率分布，如对于有监督学习我们希望学习到\(P(y\vert\boldsymbol{x})\)。评价estimator和实际概率分布之间的差距的指标有bias和variance。通常我们依据最大似然估计（maximum likelihood estimation），即：若我们拟合的概率分布以\(\boldsymbol{\theta}\)为参数，则我们希望最大化

而可以证明，最大似然等价于最小化KL divergence，等价于最小化negative log-likelihood，等价于最小化交叉熵。

前些年十分火的一种机器学习算法是 支持向量机SVM，

其中\(k\)称为 kernel，是某个内积空间的内积。比较常见的是Gaussian kernel，或radial basis function kernel，它将特征空间扩展到无穷维。

SVM的问题在于，其参数数量、训练所需的时间与训练集大小成正比，无法应对大规模的训练集。而神经网络利用随机梯度下降，训练时间复杂度与训练集大小没有紧的正比关系。同时，SVM等传统机器学习算法有无法很好地学习非连续函数等缺点，已渐渐被 deep learning 取代。

EOF